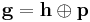Isoparametric manifold

In Riemannian geometry, an isoparametric manifold is a type of (immersed) submanifold of Euclidean space whose normal bundle is flat and whose principal curvatures are constant along any parallel normal vector field. The set of isoparametric manifolds is stable under the mean curvature flow.

Examples

The simplest example of an isoparametric manifold is a sphere in Euclidean space.

Another example is as follows. Suppose that G is a Lie group and G/H is a symmetric space with canonical decomposition

$\mathbf{g} = \mathbf{h}\oplus\mathbf{p}$

of the Lie algebra g of G into a direct sum (orthogonal with respect to the Killing form) of the Lie algebra h or H with a complementary subspace p. Then an orbit of the adjoint representation of H on p is an isoparametric manifold in p.

Ferus, D, Karcher, H, and Münzner, HF (1981). "Cliffordalgebren und neue isoparametrische Hyperflächen". Math. Z. 177 (4): 479–502. doi:10.1007/BF01219082.
Palais, RS and Terng, C-L (1987). "A general theory of canonical forms". Transactions of the American Mathematical Society (Transactions of the American Mathematical Society, Vol. 300, No. 2) 300 (2): 771–789. doi:10.2307/2000369. JSTOR 2000369.
Terng, C-L (1985). "Isoparametric submanifolds and their Coxeter groups". J. Differential Geometry 21: 79–107.